Preparation

Read Seung, H.S., 1996. How the brain keeps the eyes still. PNAS 93(23):13339-13344.

The brain can hold the eyes still because it stores a memory of eye position.  The brain’s memory of horizontal eye position is stored by persistent neural activity in a network known as the “neural integrator,” which is located in the brainstem and cerebellum.  The observed persistent patterns of activity can be interpreted from the perspective of dynamical systems as an attractive line of fixed points in the neural integrator’s state space.  [Sebastian Seung, 1996; paraphrased]

Horizontal eye position is controlled by two extra ocular eye muscles (lateral and medial recti) that are innervated by motor neurons in the abducens and oculomotor nuclei, respectively.  Motor nuclei “read out” a memory of eye position that is stored in premotor areas, namely, the medical vestibular nucleus (MVN) and prepositus hyoglossi (PH).

“memory network” vs. “neural integrator”:  When the head is still, the feedforward inputs to the network are constant, and the network is an autonomous dynamical system amenable to state space analysis.  This is the “how the brain keeps the eyes still” limit. During normal behavior, the network receives time-varying vestibular and visual input, and is a driven system rather than an autonomous one.  This is Robinson’s “integrating with neurons” situation.

Seung discusses the state space portraits of the eye position memory network, modeled as a line attractor, while the read-out network flows toward a point attractor, the location of which is determined by the state of the memory network.

As in our previous reading by Robinson, Seung discusses how positive feedback changes the time constant of persistent activity.   Seung also discusses the issue of “fine tuning” and the idea that synaptic weights could be adjusted through a learning rule.

Linear attractor networks

The simplest network models are completely linear and a natural extension of the Wilson-Cowan formalism discussed last time.  The mathematical formalism of attractor networks is summarized in this PDF.

When a linear network is written in terms of firing rate, the Wilson-Cowan equations are

.

Steady states are given by solutions of the following linear algebraic system:

In the generic case, the matrix is full rank and, regardless of , there is only one solution, a fixed point given by

If the real part of the eigenvalues of  are all negative, this is a globally asymptotically stable fixed point, i.e., the type of steady state Seung refers to as a point attractor.   Below is shown the firing rates of three neurons in a point attractor  network.  Regardless of initial condition, the same steady state is approached asymptotically.

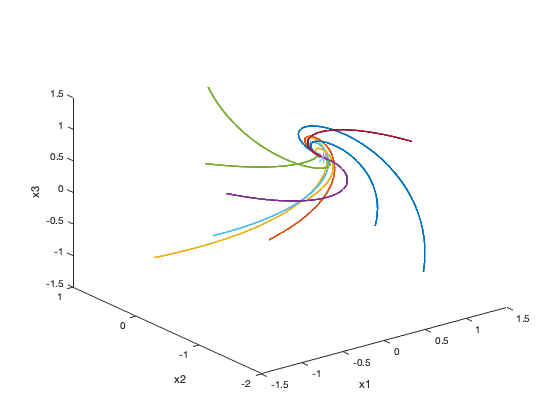
The special case of interest to Seung is when the matrix has rank (i.e., its nullity is 1) and is in the range of .  One eigenvalue of  is zero, while the other eigenvalues are negative.  In this case, there are an infinite number of stable steady states arranged as a line (a line attractor).   Different initial conditions limit on this line, but not necessarily to the same point.

Here is the matlab script that made the above figures.

% how the brain keeps the eyes still
% example linear network models

clear; close; clc

% n is number of neurons (you can change this)
n=4;

% the deficiency of rank you want 
% point attractors when nullity=0
% line attractors when nullity=1
nullity=0; 


dt = 0.001; % time step
tau = 1; % time constant 

% construct random matrix of rank N minus nullity (this is M=-I+W)
% and make sure real part of eigenvalus is negative 
M = zeros(n,n);
while any(real(eigs(M))>=0)
   M = zeros(n,n);
   for i=1:n-nullity
      M = M + randn(n,1)*randn(1,n);
   end
end
% this makes sure b is in range of M
z = orth(M); b = z*randn(size(z,2),1); 

for k=1:10 % number of initial conditions 
   x = randn(n,1);
   for i = 1:1e5
      x(:,i+1) = x(:,i)+dt/tau*(M*x(:,i)+b); % M=-I+W
   end

   % only the 2 or 3 first dimensions are plotted 
   % (x1, x2) if n=2, (x1, x2, x3) if n>=3 
   if n<=2
      plot(x(1,:),x(2,:)); hold on;
      plot(x(1,end),x(2,end),'*','MarkerSize',10);
   else
      plot3(x(1,:),x(2,:),x(3,:),'LineWidth',2); hold on;
      plot3(x(1,end),x(2,end),x(3,end),'*','MarkerSize',10); hold on;
      zlabel('x3') 
   end
   xlabel('x1')
   ylabel('x2')
end

Further reading